© Сергей С. Лачинян
Нумерология без Мистики. Откуда числа-то берутся?
Авторское название: “Эссе о Визуализации и Математизации кулинарных рецептов”; /посвящается Игорю. В. для лучшего взаимопонимания…/ «Динамическая линейка» или откуда берутся числа.
Часть 1. О Мере …
Для начала напомню – как на уровне очень глубокой аксиоматики (т.е. на постулатах, данных нам в ощущениях!) определяется само понятие числа.
Для этого берут, некую прямую линию… берут на ней некий отрезок, а затем рассуждают: … а сколько раз этот отрезок уложится на другом отрезке? Вот именно это и есть мера, или то самое — математическое число.
К этому иногда (как правило в начальных классах) добавляют зримо осязаемые образы: например камушки, палочки и тому подобные объекты.
А после этого выясняют, сколько таких палочек (камушков) содержится в некой «кучке».
И тут очень наглядно показывается, что одну «палочку» от другой, мы можем легко отличить по её внешней ГРАНИЦЕ. Или, в более общем случае, по ПРОТЯЖЕННОСТИ и свойствам ПРОСТРАНСТВА.
Если рассмотреть этот вопрос более детально, то мы опять же (как ни странно…) вернемся к первому примеру с линиями и отрезками.
Соответственно, из такого первичного определения числа, сиречь из понимания о количестве уложившихся отрезков, нам и следует далее исходить, как из самого фундаментального и данного нам в ощущениях. /…Помните мультфильм, где звери рассуждали: “сколько попугаев уложится в одном удаве:)) – А.К./
При этом утверждения разных “алгебраистов”, что числа – это сугубо абстрактное понятие (т.е. нечто, не связанное ни с какими физическими/пространственными проявлениями – типа тех, данных нам в чувствах ощущений, при соизмерении), то это … не более чем старческий маразм!
Алгебраисты просто забыли то время, когда сами были детьми, и когда иного способа, определяющего понятие числа, кроме СОИЗМЕРЕНИЯ отрезков, основанного на пространственных ощущениях, они не имели, и даже много позже, не видели в Природе, ни, увы, не мыслили в своих головах.
Хотя, конечно, если постараться и забыть все первоисточники наших постулатов, то … тогда можно считать понятие числа абстрактной, самостоятельной и даже невесть откуда взявшейся сущностью…
Но непонятно, куда при этом деваться от «скрытых» аксиом, данных нам в наших же детских ощущениях и не сводимых ни к каким иным первопричинам?
Часть 2. Соизмерение
Вот к соизмерениям, как к первопричинам мы теперь и обратимся.
Поставим вопрос так: а существуют ли в условиях окружающей нас естественной природы механизмы такого соизмерения? Или такого рода соизмерения – только продукт манипуляций в головах школяров и мат ,е,МАТИКОВ.
Главное тут понять один важный нюанс.
Для того чтобы отложить один отрезок на другом, кроме самых отрезков и «абстрактного» понятия чисел нам (неявно для математиков) требуется еще одна важная сущность – особая процедура (процесс) “откладывания” одного на другом, который в физике прозаически называется … (ВЗАИМО)ДЕЙСТВИЕ.
То есть, мы должны уразуметь что понятие числа … не может появиться без физических пространственных мер и скрытого от глаз, точнее от математического ума, физического взаимодействия отрезков.
А ведь это – еще одна скрытая аксиома – или постулат, данный нам в ощущениях, и о-о-о-о-очень плохо осознаваемый большинством людей, рассуждающих о математике и числах.
Отсюда мы и приходим к не оригинальному выводу, что крайне абстрактное понятие ЧИСЛА опирается на крайне осязаемые (данные нам в ощущениях) понятия протяженности и взаимодействия (в более общем случае меры этого взаимодействия приведенной к «объему» — т.е. протяженности).
Следовательно, на вопрос – существуют ли числа в природе,
мы даем положительный ответ:
КОНЕЧНО ЖЕ – ДА!
И заключается это утверждение о ЧИСЛАХ на банальной идее существования физической меры, (количестве) “вложенностей” одного в другом….
Ну а теперь нам надо было бы попытаться найти тот универсальный природный «метр», некую природную единицу измерения, чтобы вся математика могла бы запросто «выводится» из преобразований этого «метра». Причём, непосредственно в самой Природе — желательно без нашего умственного участия.
Если конечно она – Природа — не станет противоречить такой нашей природной математике, то тогда мы всю известную математику сможем “выводить” из показаний вольтметров и синхрофазотронов.
Но, тут, пожалуйста, спросите себя: а чем, собственно, заняты наши физики сегодня? И, покопавшись в трактатах, вы поймёте, что, как ни странно, … физики заняты совершенно обратным процессом, они выводят всю окружающую нас реальность из абстрактных понятий математики (да еще не перестают при том удивляться, как это такая «абстрактная» математика, так хорошо описывает нашу материальную реальность…) .
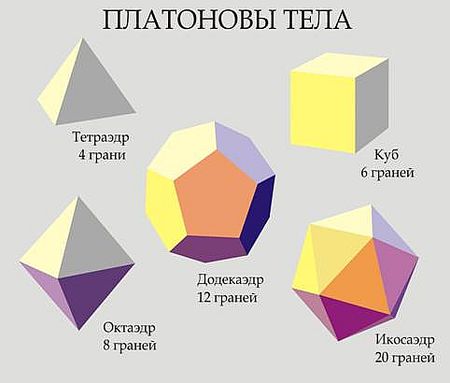
Конечно, соблазн найти математику в природе велик, и многие, видимо поэтому (см. выше), ищут некую фундаментальную длину, (правильнее конечно было бы искать фундаментальный объем, а далее (и, как следствие), те фундаментальные формы, которые этот объем содержат…
В частности, вплоть до фигур Платона и его Платоновских тел…).
Однако, есть серьезные основания полагать, что Истина в чем то ином, не сводящемся к манипуляциям с числами, но как всегда, где-то рядом…
Часть 3. Физический прототип
Если присмотреться внимательно к вопросу соизмерения, то обнаруживается очень простое физическое явление, которое не только обеспечивает действие СОИЗМЕРЕНИЯ, но и наилучшим образом определяет саму МЕРУ этого действия!
Что же это за физическое явление?
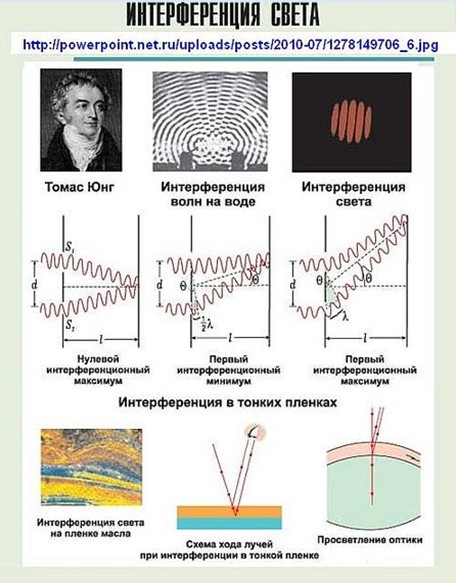
А это …весьма обыденная и широко известная со школьных лет интерференция волн.
Действительно, при ближайшем рассмотрении интерференция и есть ни что иное, как автоматическое определение того, сколько раз один отрезок (волна №1) укладывается на другом (волна №2).
Рис.1
А итоговый результат такого соизмерения мы мгновенно получаем во всем возможном его математическом многообразии.
Начиная от сумм и разностей и кончая кратностями и производными фрактальными и пр. множествами.
Формула
Весьма дорого нашему сердцу в этом новом представлении будет то, что результат “сопоставления”, абсолютно независим от длины волн и их природы (происхождения) и выражается строго в том фундаментальном детском представлении о числе — что и сколько раз, друг на друге откладывается.
Более того, он представим для нас в самом удобочитаемом виде – будь то цвет (если интерферировали световые волны), музыка♫, либо тембр (если интерферировали акустические колебания), или, наконец, банальное ЧИСЛО, (если осуществлялась интерференция абстрактных отрезков в наших головах).
Очень важно, что наличие такой относительной, динамической меры приводит к тому, что при трансляции (переносе), например при умножении или делении на любое целое число — скажем на коэффициент 2n длинны этих волн, результат (что, в чем и сколько раз уложилось) не меняется!
А это значит, что если мы хотим услышать или увидеть очень медленные или очень быстрые волны, то их достаточно транспонировать в иной более удобный для нас частотный диапазон. А еще это значит, что все в мире, начиная от периодов движения планет, до звуков и света — все подчинено одним и тем же законам числовых отношений — которые мы в итоге называем МАТЕМАТИКОЙ.
А само ЧИСЛО, как результат специфической “интерференции”, при этом будет всегда инвариантно… (то есть, не зависеть от конкретных физических величин, природы или длины волн, поскольку мы имеем их отношения).
Вот это и есть, действительно универсальный природный «МЕТР».
Да еще обладающий той уникальной особенностью, что из таких природных чисел, являющихся первопричиной меры и пространственных отношений, автоматически выводится абсолютно вся существующая и несуществующая математика.
А если сильно захотите, то даже и математика без всяких математических формул!
Кроме того, весьма важно, что такое ЧИСЛО, дано нам в человеческих ощущениях, и потому существует феномен музыки, как естественный математический язык.
Соответственно, мы понимаем, музыка – это высшая математика (без формул…), но выраженная понятным нам ЯЗЫКОМ физических взаимодействий.
Это – особый язык звуков, отражающий всю гамму математической сути, числа и меры, качеств и их преобразований.
Конечно же такое понимание математики и ЯЗЫКОВ (а математика это только – частный случай языка) в науке, увы, пока не принято.
А главными причинами тому является:
1) засилье дискретного мышления и
2) крохоборствующие аналитики, которые, имея творческую микросилу, могут сконструировать нечто целое, исключительно лишь путём кропотливого “складывания” в кучки соответствующих микрочастиц, для чего применяется «универсальный» метод познания, известный с первобытных времен — большая дубина (см. до какой гигантской дубины дошли с коллайдерами) и дробление на эти самые частицы и «кучки».
Или, говоря тезисами нашего Эссе, ученые способны воспринимать музыку … только с линейкой и арифмометром, вычисляя и меряя в “Оркестре Истины” каждую отдельную вырванную ноту (волну), поскольку сознание таких учёных “окуклилось” уже во времена начальной школы, с момента первых “соизмерений” отрезков или счета камушков в кучках.
Часть 4. Нумерология
А здесь я сейчас я напишу страшную вещь! Трепещите Атеисты и Ма тераз матики!
Числа имеют свойства и качества, как то: цвет, вкус, и даже … строгие соответствия определенным датам и/или характерам.
Сказанное выше – это уже не математика, а предмет самой, что ни на есть, нумерологии!
Хотите доказательства!
Так они уже представлены!
Вспомните. Каждое соотношение волн (например, музыкальный интервал), отражается во вполне конкретных ФИЗИЧЕСКИХ свойствах, качествах и действиях — от результирующего цвета и тембра, до каких-либо известных нам химических и физических свойств элементов определяемых интерференцией их волн (посмотрите спектрограммы в химии и астрономии…).
Последние, в частности, определяются энергией связи или взаимодействием внешних электронов (волны). Причём, то и другое выражается через частоты или длину этой волны, что хорошо известно студентам из формул типа E= h 1/T .
Эта же зависимость благополучно проявляется во вкусах, цветах, запахах, энергиях и спектрах вещества, астрономических явлениях или биоритмах.
Но, тогда получается, что каждое взаимодействие в Природе, это в конечном итоге просто … интерференции (СОИЗМЕРЕНИЕ) некоторого рода волн, а результат такой интерференции — это физическое ЧИСЛО или МЕРА, которое (ЧИСЛО) и определяет свойства и результаты любого взаимодействия, характер происходящих явлений, их причины и следствия. Везде мы видим «абстрактное» число — сложение и вычитание волн. Порождающих многообразие мира, включая таблицу химических элементов. И, в конечном итоге, всю наблюдаемую нами физическую Вселенную.
Если взаимодействие гармонично – то это будет синтез или рождение соизмеримого — гармония (когда соизмерение/интерференции кратны на большинстве суммарно разностных частот). И при такой гармонии мы получаем известные нам МУЗЫКАЛЬНЫЕ интервалы и саму музыку как феномен.
А ежели взаимодействие диссонансное (когда отношения иррациональны) то мы приходим к движениям, трансформациям, и переменам, а по китайским воззрениям жить во время перемен это к неприятностям.
И при этом совсем не важно – будут ли это молекулы вещества, ваша Судьба, Звезды или фальшивые ноты в оркестре.
Вот откуда можно легко понять, что одни числа очень “подходят” друг другу (гармоничны), другие … ни в коем разе (они диссонансные), одни везунчики, другие лузеры! Одни числа рождают связь, другие ее разрушают, одни сладкие, другие кислые, теплые или фиолетовые…
И цвета и ноты и силы, так же связаны с вполне определенными числами и их отношениями! Потому нет ничего полезнее в кулинарии, чем знание законов о числах (соотношения ритмов и качеств). Вот только, вряд ли десятичное исчисление и кропотливое складывание значащих десятичных цифр («корень числа»), может быть основой Нумерологии, ведь музыка подчиняется другим мерам (учите мат.часть!).
Так, запросто, мы убеждаемся, что числа, оказывается имеют свой НЕОТЪЕМЛЕМЫЙ СМЫСЛ и КАЧЕСТВА, которые, влияют на всякие события (взаимодействия), на свойства и характеры, и на все окружающее нас в реальности.
Включая сюда, естественно, и Судьбу, которая – суть, взаимодействие разных качеств, событий и людей…
Вот и получается в чистом виде НУМЕРОЛОГИЯ, а еще и … Кузькина мать, в придачу — к «жаренной математике».
Часть 5. Мораль
Тот, кто постигнет душу музыки или музыкальную гармонию – тот и есть самый высший Математик и Пророк.
Именно к этому и призывали всех нас изо всех своих “доисторических” сил, не такие уж глупые, как наконец выясняется, пифагорейцы.
За что всем им – наш пламенный Привет!
С большим МУЗЫКАЛЬНЫМ приветом ко всем остальным, включая своих современников
27.11.2008г.
Сергей Суренович Лачинян
Казахстан, Алма-Ата, sergeyluch@tutanota.com
Примечание: Иллюстрации к интернет варианту данной статьи подобраны Сергеем Алферовым.
Ниже приведены отрывки из статьи «Классификатор на основе фундаментального инварианта». В частности глава, где даны основные соотношения натурального музыкального ряда, как отношений интервалов, которые дают целочисленные и кратные первичным частотам производные гармоники.

…..
 Примечание: В формуле 3.6. допущена небольшая неточность, которую может исправить любой школьник.
Примечание: В формуле 3.6. допущена небольшая неточность, которую может исправить любой школьник.
P. S. Для иллюстрации сказанного приведу простейший пример. Известно, что существует загадка «золотого сечения», некого числа 1,618… которое «всплывает» как мерило гармонии или математическое отношение в самых «неожиданных» местах.
И вокруг которого существует множество мистических измышлений.
Если исходить из сказанного в этом эссе, то можно с легкостью раскрыть не только содержание этого числа, но и указать его прямую связь с физическим миром. По сути это оказывается просто результат интерференции двух произвольных частот и их суммарно разностных гармоник, интерференция которых (отношение их частот друг к другу — представляющее ряд Фибоначчи) дает в итоге «золотое сечение». А следствием этих интерференций и их закономерностей (принципа соизмерения) будет проявление их как известные нам свойства пространства/времени и закономерности физических процессов или соотношений в пространстве и геометрия (то есть, интерференция волн это причина, а свойства пространства — а так же физика и математика — как абстракции созданные вокруг операций соизмерения, это уже следствия).
Привожу выдержку из своих более ранних работ на эту тему — «Классификатор на основе фундаментального инварианта.»
«… Более того, единственным известным нам естественным явлением соизмерения в физическом мире, является наложение и интерференция волн. Известно, что мышление человека, искусственные и естественные языки (включая математику и т. п.), а также миро постижение в целом, построены на процедуре соизмерения. Соответственно, рассматривая циклы (волновые процессы) как механизм соизмерения, можно установить взаимно однозначное соответствие между числом или мерой (результат соизмерения и основа математик), пространством и временем (атрибуты волнового процесса и основа геометрии), и мышлением (мировоззрение и языки).
Таким образом, удается раскрыть «мистическую» связь математики и физической реальности, а также раскрыть и развить физический смысл геометрий. Кроме того, появляется возможность построить математику качеств, поскольку качества это, колебания и силы (волны, вращения и их преобразования) или соответственно, интерференции, соотношения частот и спектры. Далее, в геометрической проекции сложение (интерференция) колебаний и вращений обуславливает формы и структуры. Столь же очевидно, в голографической логике, интерпретируется феномены пространственных симметрий. Например, феномен «Золотого сечения», поскольку это ни что иное, как величина, к которой стремиться отношение частот суммарно разностных гармоник составляющих известный ряд Фибоначчи: f1+f2=f3; f2+f3=f5; f3+f5=f8; f5+f8=f13 … fn+fm=fz; где
fm/fn=1,618… при m и n стремящихся к бесконечности.
Или в физической интерпретации: «Золотое сечение» это зримый (математический и геометрический) результат интерференции волн в системе с высокой добротностью. Излишне говорить сколь широко встречается «Золотое сечение» в природе, и насколько важно понимание физического смысла подобных симметрий.
В приложении к искусственным языкам и техническим средствам их обработки, таким как компьютерная техника, методы голографической логики позволяют обеспечить решение проблемы взаимного соответствия между языком и естественным многообразием явлений или естественным мировосприятием человека. Следовательно, позволяют решить проблему классификации и упорядочения информации. В качестве иллюстрации способов упорядочения и соизмерения разнородных понятий из областей Геометрии, Физики, Социологии, Астрологии, Лингвистики, музыкальных закономерностей и т.д. можно представить следующие схемы[1]:»
[1] См. С. Лачинян «Созидающие технологии».
С. Лачинян 22 января 2004 г.